Descubra como a geometria espacial pode aparecer no Enem

A prova de matemática do Exame Nacional do Ensino Médio (Enem) possui 45 questões que exigem dos alunos uma boa interpretação de gráficos, tabelas e entendimento dos enunciados. Mas há áreas específicas que precisam de uma atenção especial. É o caso da geometria espacial.

Essa parte da matemática aparece, principalmente, em tópicos relacionados ao estudo dos cilindros, paralelepípedos e cubos.

A geometria espacial é a área da matemática responsável pelo estudo dos sólidos geométricos e a geometria no espaço. Para os alunos que irão realizar o exame neste ano, precisam compreender e calcular o volume e a dimensão de cada um desses objetivos.

O professor de matemática Ronaebson Ferreira, do EstudoPlay, separou algumas dicas para os alunos que vão realizar o Enem este ano.

“Os assuntos que os alunos devem priorizar em geometria espacial são cilindro, paralelepípedo e cubo. Esses são os mais cobrados. Naturalmente, o que se valoriza é a parte do volume”, destaca o professor.

Elementos primitivos

• Ponto: é a base da geometria, já que, todas as figuras geométricas são consideradas como um conjunto de pontos;
• Reta: composta por pontos, não possui origem, nem dimensão e pode ser considerada infinita. Dessa forma, não é possível considerar o seu comprimento;
• Linha: ela possui algumas semelhanças com a reta, já que, também, é considerada infinita. Entretanto, tem a possibilidade de formar curvas;
• Plano: corresponde ao enfileiramento de retas e é onde as figuras bidimensionais são construídas, em uma superfície plana.

Fórmulas

O professor Ronaebson Ferreira afirma que as principais fórmulas para o Enem são a do volume do paralelepípedo e a do cilindro.

O cilindro é caracterizado por possuir uma base circular, Dessa forma, o seu volume depende somente da altura (h) e do raio (r) do objeto.

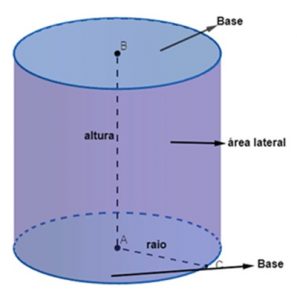
V = πr² ·h

At = 2πr ( r + h)

Al → área lateral

O paralelepípedo é um sólido geométrico formado por faces no formato de paralelogramos. Para calcular o seu volume é necessário analisar a sua altura (a) , largura (b) e comprimento (C).

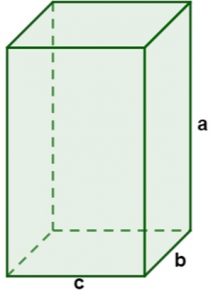
V=a.b.c
AT= 2ab + 2ac + 2bc